France Location on World Map

Demystifying the Karnaugh Map: A Comprehensive Guide to Logic Simplification

Related Articles: Demystifying the Karnaugh Map: A Comprehensive Guide to Logic Simplification

Introduction

With great pleasure, we will explore the intriguing topic related to Demystifying the Karnaugh Map: A Comprehensive Guide to Logic Simplification. Let’s weave interesting information and offer fresh perspectives to the readers.

Demystifying the Karnaugh Map: A Comprehensive Guide to Logic Simplification

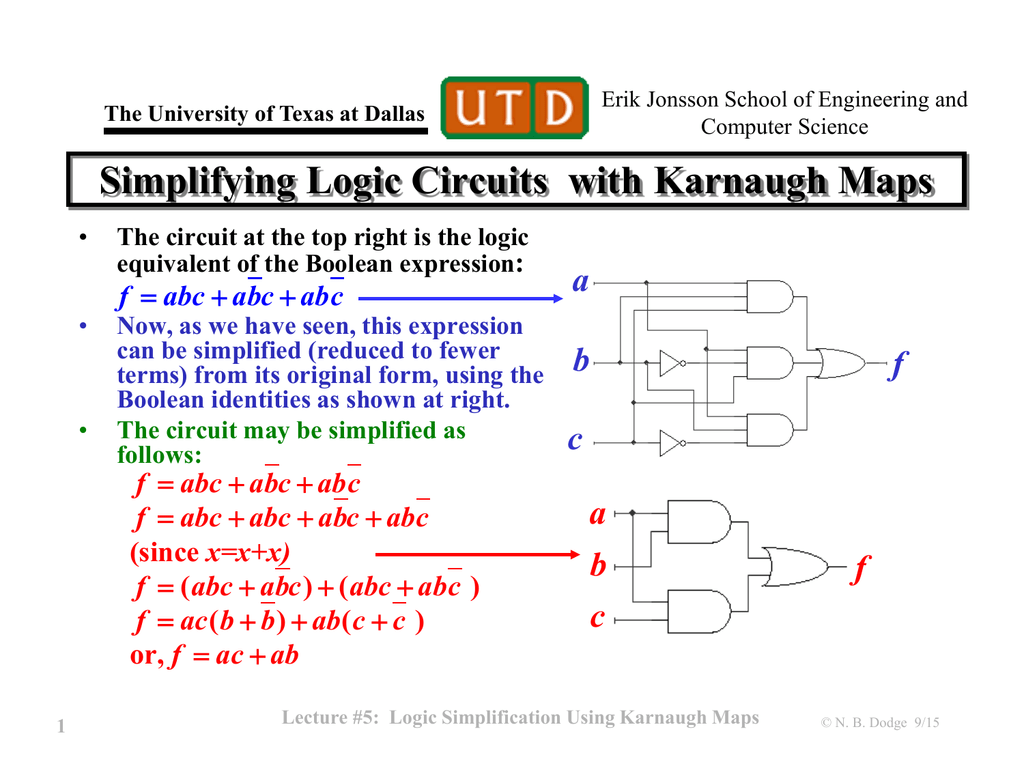
The realm of digital logic design is often characterized by intricate Boolean expressions, representing complex relationships between input and output signals. Simplifying these expressions is paramount, as it leads to more efficient circuit implementations, reducing cost, power consumption, and component count. Enter the Karnaugh map (K-map), a powerful visual tool that facilitates the simplification of Boolean functions, offering a systematic approach to logic optimization.

Understanding the Essence of Karnaugh Maps

At its core, a K-map is a graphical representation of a truth table, employing a specific arrangement of cells to depict the output values for all possible input combinations. Each cell corresponds to a unique minterm (a product term representing a specific input combination) within the truth table. The arrangement of cells is crucial, as it ensures that adjacent cells differ in only one input variable. This arrangement, known as the Gray code ordering, is instrumental in identifying and grouping adjacent cells representing "don’t care" conditions, leading to the simplification of the Boolean expression.

Constructing a Karnaugh Map: A Step-by-Step Approach

1. Define the Number of Variables: The first step involves determining the number of input variables (n) in the Boolean function. This dictates the size of the K-map, requiring 2^n cells. For instance, a function with three input variables necessitates an 8-cell K-map (2^3 = 8).

2. Assign Binary Values to Input Variables: Each cell in the K-map represents a unique combination of input variables. The cells are labeled with binary values, following the Gray code ordering, ensuring adjacent cells differ in only one bit. This ordering simplifies the identification of adjacent cells for grouping.

3. Populate the Map with Output Values: The output values from the truth table are then entered into the corresponding cells of the K-map. Each cell’s output value represents the Boolean function’s output for the input combination associated with that cell.

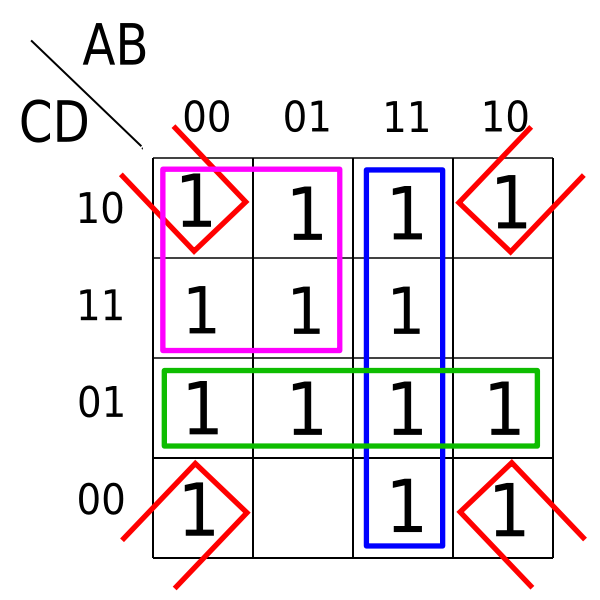
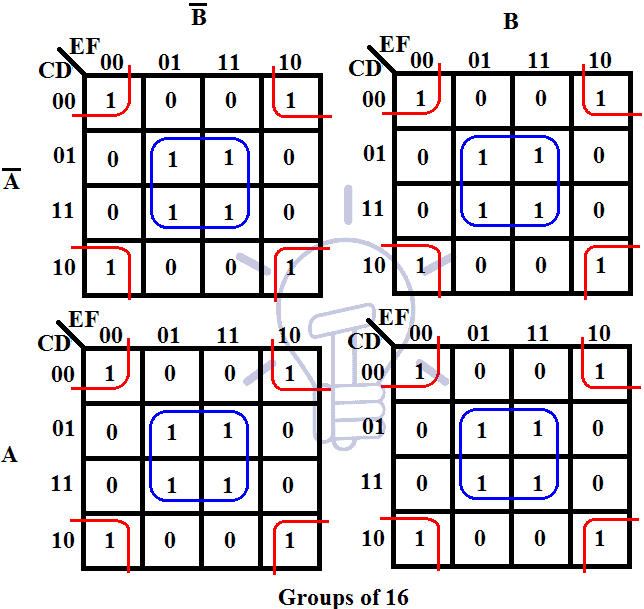
4. Group Adjacent Cells with ‘1’s: The key to simplifying the Boolean function lies in grouping adjacent cells containing ‘1’s. These groups must be rectangular or square, with dimensions that are powers of two (1, 2, 4, 8, etc.). Larger groups lead to simpler expressions, as they represent fewer input variables in the resulting product term.

5. Identify and Utilize ‘Don’t Care’ Conditions: In some cases, the truth table may include "don’t care" conditions, denoted by ‘X’. These conditions represent input combinations that are not relevant to the function’s operation. ‘Don’t care’ conditions can be included in groups to further simplify the expression.

Simplifying Boolean Expressions: The Power of K-Maps

Once the K-map is constructed and the adjacent cells are grouped, the simplification process begins. Each group corresponds to a product term in the simplified expression. The variables in each product term are determined by identifying the input variables that remain constant within the group.

• Sum of Products (SOP): If the groups contain ‘1’s, the simplified expression is obtained by summing the product terms corresponding to each group.

• Product of Sums (POS): If the groups contain ‘0’s, the simplified expression is obtained by multiplying the sum terms corresponding to each group.

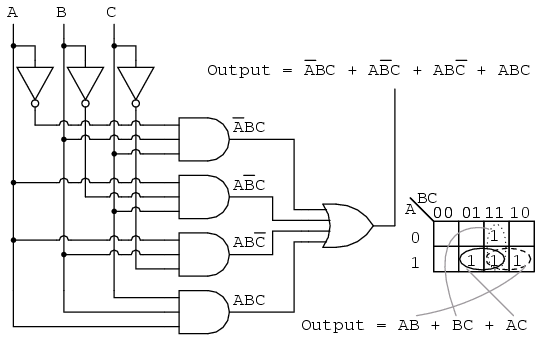
Illustrative Example: Simplifying a Boolean Function

Consider the following Boolean function:

F(A, B, C) = Σ(0, 2, 4, 6)

This expression represents a function with three input variables (A, B, C) and outputs ‘1’ for the minterms 0, 2, 4, and 6.

1. Construct the K-map: A 3-variable K-map with 8 cells is created, with each cell representing a unique combination of A, B, and C.

2. Populate with Output Values: The cells corresponding to minterms 0, 2, 4, and 6 are filled with ‘1’s. The remaining cells are filled with ‘0’s.

3. Group Adjacent Cells: Two groups are formed: one containing cells 0 and 2, and another containing cells 4 and 6.

4. Simplify the Expression:

   • The group containing cells 0 and 2 represents the product term A’C’.
   • The group containing cells 4 and 6 represents the product term BC’.

5. Final Simplified Expression: The simplified expression in SOP form is:

F(A, B, C) = A'C' + BC'

This expression is significantly simpler than the original expression, representing a more efficient circuit implementation.

Advantages of Using Karnaugh Maps

1. Visual Simplification: The K-map provides a visual representation of the Boolean function, making the simplification process more intuitive and less prone to errors.

2. Systematic Approach: The K-map offers a structured approach to simplifying Boolean expressions, ensuring all possible simplifications are considered.

3. Efficiency: The use of adjacent cell grouping and ‘don’t care’ conditions leads to efficient circuit implementations, minimizing the number of logic gates required.

4. Error Reduction: The visual nature of the K-map helps identify and correct potential errors in the simplification process.

FAQs Regarding Karnaugh Maps

Q: What are the limitations of Karnaugh maps?

A: K-maps are best suited for simplifying functions with a limited number of input variables. As the number of variables increases, the size of the map grows exponentially, making it cumbersome and impractical.

Q: Can K-maps be used for functions with more than four variables?

A: While K-maps can be extended to handle functions with more than four variables, the process becomes increasingly complex and difficult to visualize. For functions with five or more variables, alternative methods like the Quine-McCluskey algorithm are typically employed.

Q: How do ‘don’t care’ conditions impact K-map simplification?

A: ‘Don’t care’ conditions provide flexibility in grouping cells, potentially leading to further simplification of the Boolean expression. They can be included in groups to maximize their size, resulting in a more efficient circuit implementation.

Tips for Effective Karnaugh Map Usage

1. Understand Gray Code Ordering: Familiarity with Gray code ordering is essential for correctly identifying adjacent cells for grouping.

2. Utilize ‘Don’t Care’ Conditions: Actively seek out and utilize ‘don’t care’ conditions to enhance simplification.

3. Prioritize Larger Groups: Aim to form the largest possible groups to minimize the number of product terms in the simplified expression.

4. Consider Both SOP and POS Forms: Evaluate the simplified expressions in both SOP and POS forms to determine the most efficient implementation.

5. Practice with Different Examples: The more you practice constructing and simplifying K-maps, the more comfortable and proficient you will become.

Conclusion: The Enduring Relevance of Karnaugh Maps

In the ever-evolving landscape of digital logic design, the Karnaugh map remains a valuable tool for simplifying Boolean functions. Its visual nature and systematic approach provide a clear path to optimizing logic circuits, leading to reduced cost, improved performance, and enhanced efficiency. While alternative methods like the Quine-McCluskey algorithm are available for handling more complex functions, the K-map continues to be a cornerstone of logic design education and practice, offering a powerful and intuitive approach to logic simplification.

Closure

Thus, we hope this article has provided valuable insights into Demystifying the Karnaugh Map: A Comprehensive Guide to Logic Simplification. We appreciate your attention to our article. See you in our next article!