France Location on World Map

Unveiling the Power of Karnaugh Maps: A Comprehensive Exploration

Related Articles: Unveiling the Power of Karnaugh Maps: A Comprehensive Exploration

Introduction

With enthusiasm, let’s navigate through the intriguing topic related to Unveiling the Power of Karnaugh Maps: A Comprehensive Exploration. Let’s weave interesting information and offer fresh perspectives to the readers.

Unveiling the Power of Karnaugh Maps: A Comprehensive Exploration

The realm of digital circuit design hinges on the ability to effectively represent and manipulate Boolean expressions, which govern the behavior of logic gates. While truth tables provide a straightforward way to depict these expressions, they often lack the visual clarity needed for efficient simplification. Enter Karnaugh maps, a powerful tool that leverages visual representation to streamline Boolean simplification and optimize circuit design.

A Visual Journey into Boolean Logic:

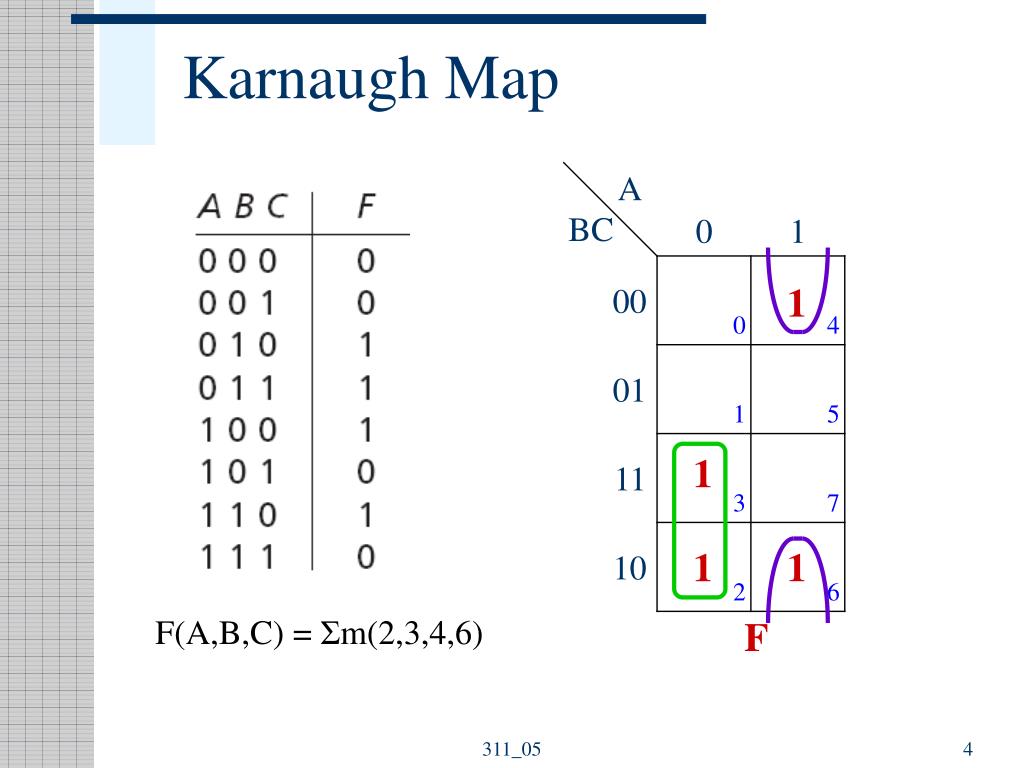
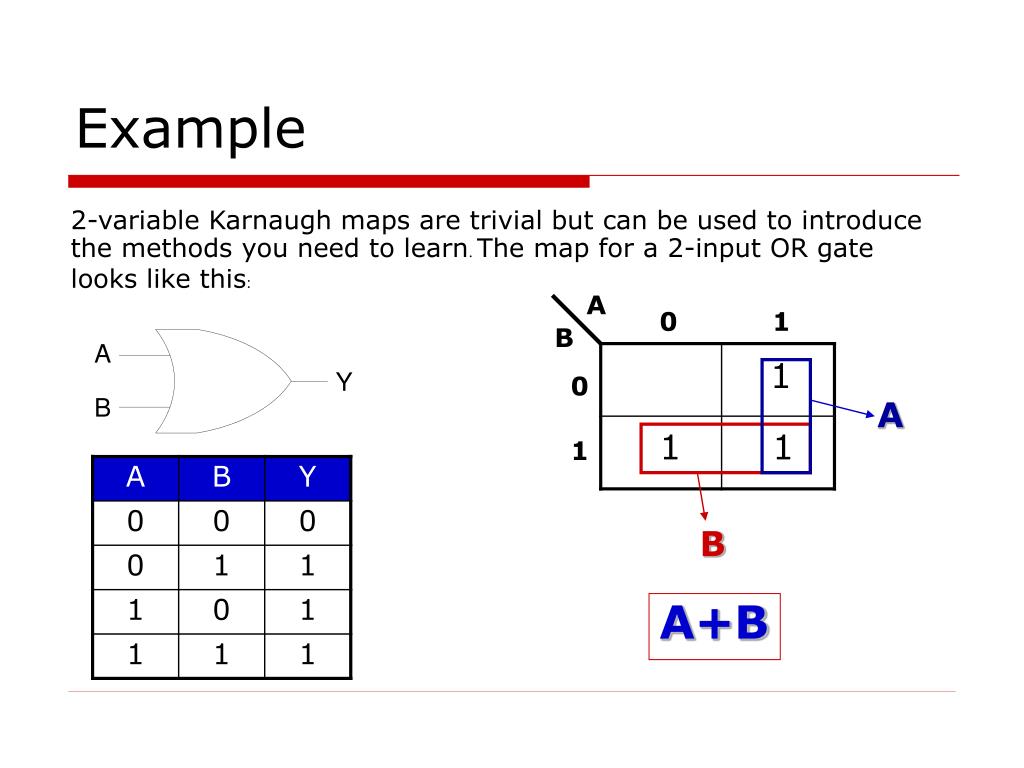
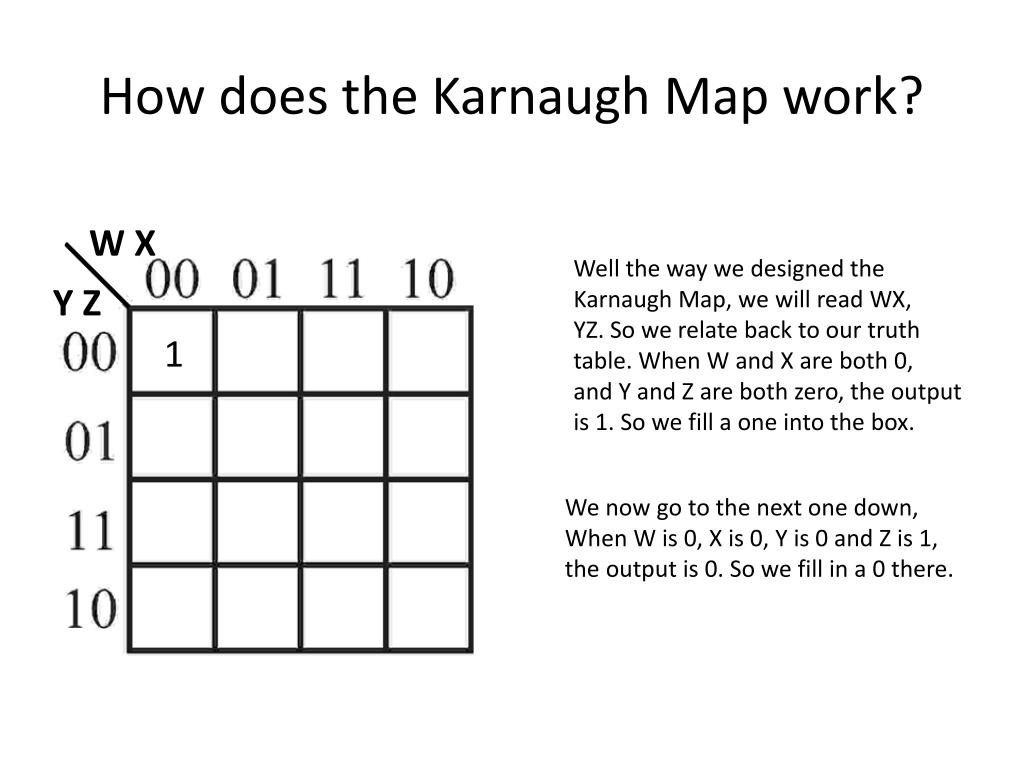
Karnaugh maps, often referred to as K-maps, are graphical representations of Boolean functions. They utilize a grid structure, where each cell corresponds to a unique combination of input variables. The arrangement of cells follows a specific pattern, ensuring adjacent cells differ by only one input variable. This arrangement is crucial for identifying and grouping adjacent cells representing "1" outputs, a key step in simplifying Boolean expressions.

Constructing the Map:

Creating a K-map begins with identifying the number of input variables in the Boolean function. Each variable requires two rows or columns in the map, representing the two possible values (0 and 1). For example, a function with three input variables (A, B, C) will have a 2x2x2 grid (2^3 = 8 cells), representing all possible combinations of A, B, and C. The rows and columns are labeled according to a Gray code sequence, where only one bit changes between adjacent cells. This ensures that adjacent cells in the map correspond to input combinations differing by only one variable.

The Art of Simplification:

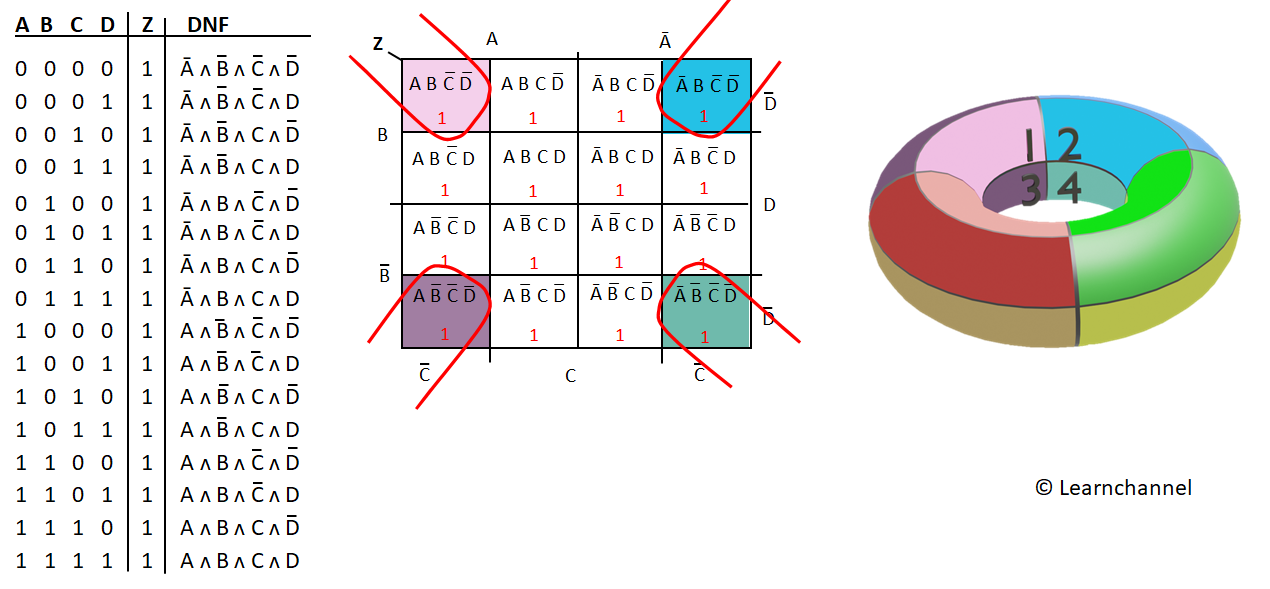
The core advantage of K-maps lies in their ability to simplify Boolean expressions visually. By grouping adjacent cells containing "1" outputs, one can identify and eliminate redundant terms in the original expression. The grouping process follows specific rules:

• Adjacent cells: Cells are considered adjacent if they share a common edge, even if they are on the opposite side of the map (due to the wrapping nature of the grid).
• Power of two: Groups should contain a number of cells that is a power of two (1, 2, 4, 8, etc.).
• Largest groups: Prioritize forming the largest possible groups, as this minimizes the number of terms in the simplified expression.

Interpreting the Groups:

Once the cells are grouped, each group represents a simplified product term in the Boolean expression. The product term is determined by identifying the variables that remain constant within the group. For example, a group of four cells where the variable A is always "1" and B is always "0" would be represented by the term "A’B".

Beyond Simplification:

K-maps are not limited to simplifying Boolean expressions. They also offer valuable insights into circuit design:

• Minimizing gates: By reducing the number of terms in the expression, K-maps minimize the number of logic gates required to implement the circuit, leading to cost savings and improved efficiency.
• Identifying don’t care conditions: In certain cases, the output of a function may be irrelevant for specific input combinations. These "don’t care" conditions can be utilized in K-maps to further simplify the expression and potentially reduce the circuit complexity.
• Visualizing logic functions: K-maps provide a clear and concise visual representation of Boolean functions, making it easier to understand and analyze their behavior.

Frequently Asked Questions about Karnaugh Maps:

1. What are the limitations of K-maps?

While powerful, K-maps become cumbersome for functions with a large number of input variables. For functions exceeding five variables, the visual representation becomes complex and difficult to manage. In such cases, other simplification methods like Quine-McCluskey algorithm or Espresso heuristic logic minimizer are employed.

2. Can K-maps handle multiple outputs?

K-maps are primarily designed for single-output functions. However, for circuits with multiple outputs, a separate K-map can be constructed for each output function.

3. How do I handle "don’t care" conditions in K-maps?

"Don’t care" conditions are marked with an "X" in the K-map. These cells can be included in any group to maximize its size, as their output value does not affect the overall function.

4. Can K-maps be used for sequential circuits?

While K-maps are primarily used for combinational circuits, they can be applied to simplify the combinational logic within sequential circuits. However, the design of sequential circuits often involves state machines and other techniques beyond the scope of K-maps.

Tips for Effective K-map Usage:

• Start with a clear Boolean expression: Ensure the expression is correctly written and understand the input and output variables.
• Choose the appropriate map size: Select a map that matches the number of input variables in the function.
• Label the rows and columns carefully: Use Gray code sequence for labeling to ensure adjacent cells differ by only one variable.
• Group cells strategically: Prioritize forming the largest possible groups, encompassing all "1" outputs.
• Double-check the simplified expression: Verify that the simplified expression matches the original function’s truth table.

Conclusion:

Karnaugh maps serve as an indispensable tool in the digital design arsenal, enabling efficient simplification of Boolean expressions and optimization of circuit design. Their visual nature provides a clear and intuitive approach to understanding and manipulating logic functions, fostering a deeper comprehension of circuit behavior. While K-maps have limitations when dealing with a large number of variables, they remain a valuable technique for simplifying logic circuits and enhancing design efficiency.

Closure

Thus, we hope this article has provided valuable insights into Unveiling the Power of Karnaugh Maps: A Comprehensive Exploration. We thank you for taking the time to read this article. See you in our next article!